First Order System Transfer Function
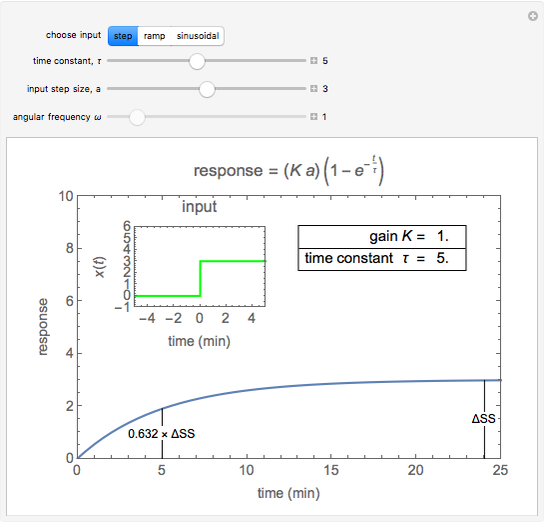
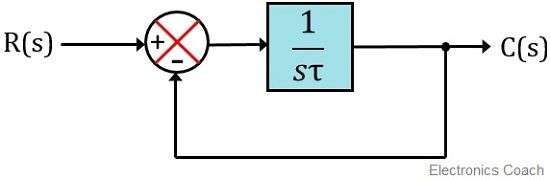
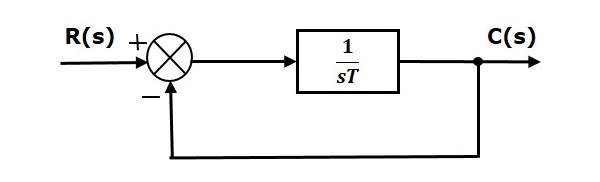
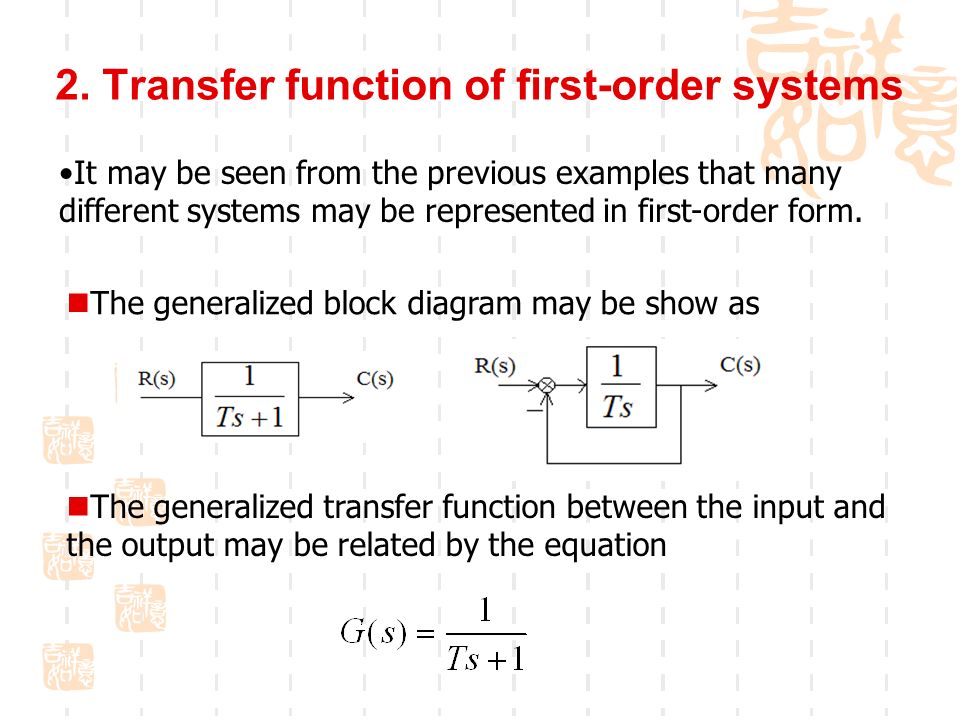
First order system transfer function. First Order Systems First order systems are systems whose dynamics are described by the transfer function where is the systems steady-state gain is the time constant First order systems are the most common behaviour encountered in practice. You can vary the magnitude of the input and the time constant τ. Gs 3 s 2 15 05s 1 a 0 2.
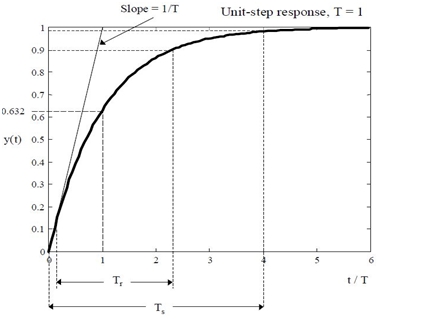
1 0 10 which has a single root 1. The time constant is related to how long a system takes to reach the new steady state. The time constant is related to how long a system takes to reach the new steady state.
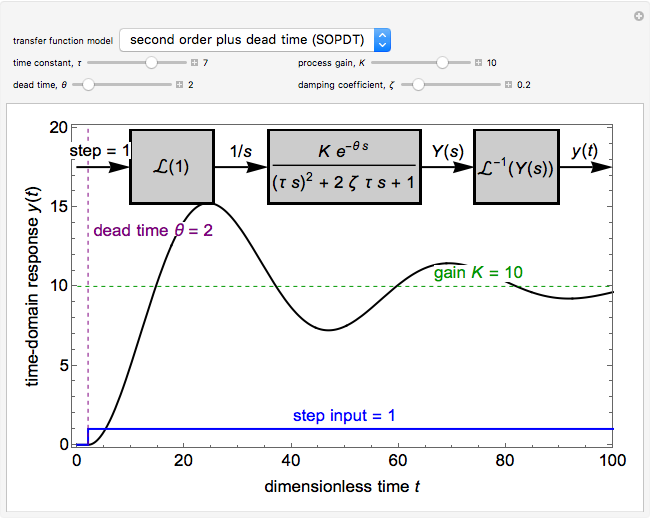
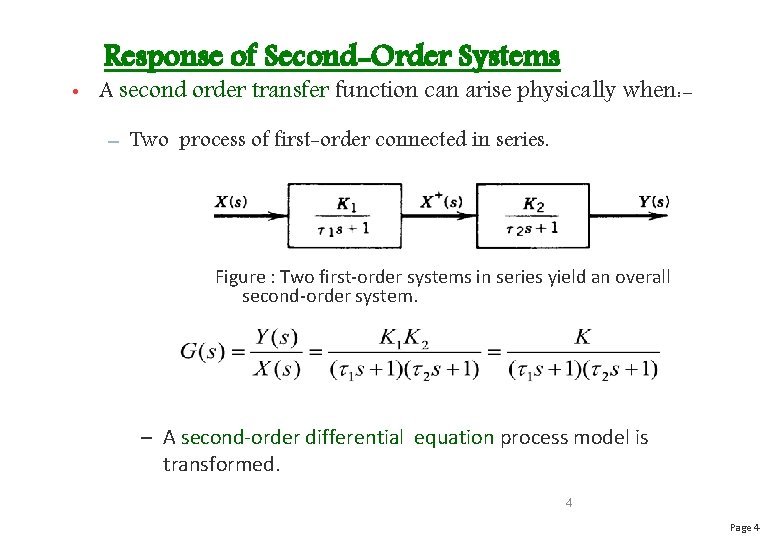
1 is the same for all system variables. This model is linear as long as ft is not a function of x thus it can be transformed into a transfer function This type of transfer function is known as a first order lag with a steady state gain of 10. PD Control of Second Order System Process and controller transfer functions Ps b s2 a1s a2 Cs kp kds Closed loop transfer function from reference to output Gyrs PC 1 PC bkds kp s2 a1 bkds a2 bkp Closed loop system of second order controller has two parameters.
Time Response of First Order Systems Consider a general rst order transfer function strictly proper Gs Gs Rs b 0 s a 0 It is common also to write Gs as Gs K s 1 b 0 s a 0 ie a 0 1. Going from a transfer function to a single nth order differential equation is equally straightforward. A first order system would only have one state equation and a.
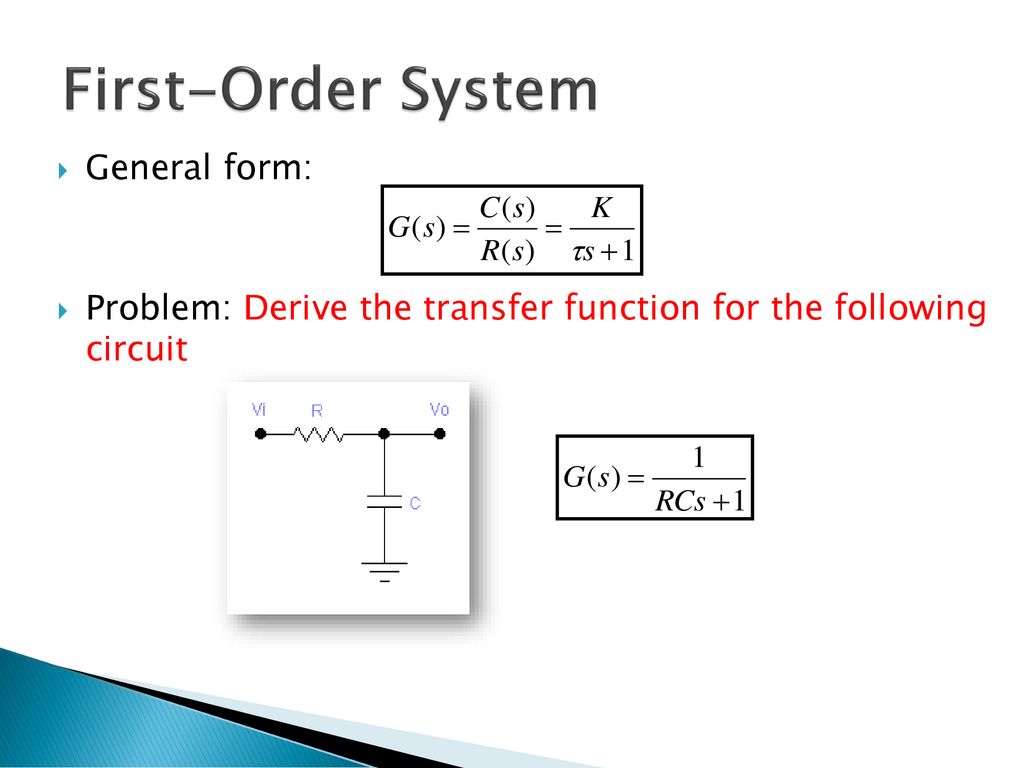
Using the transfer function generator simulate the first order system represented by. Where a b and c are arbitrary real numbers and either b or c but not both may be zero. The general first-order transfer function in the Laplace domain is.
This order gives the number of poles and - thus - determines the roll-off characteristics of the transfer function magnitude as well as the amount of phase shift for rising frequencies. Craig 8 Pade Approximation. This simulation shows the responses to a first-order transfer function.
The procedure is simply reversed. Step Response of a first order system.
Kis called the DC-gain.
All closed loop poles can be chosen but no. The general form of transfer function of first order systems Response of first order systems to some common forcing functions predict and understand how it responds to an input Time behavior of a system is important. Craig 8 Pade Approximation. Therefore the transfer function for the angular velocity is Ωs V ss 30 s2 62s300. Is called the time constant. I used transfer function as an example the same can be said if you use a State-Space model. 1 is the same for all system variables. Going from a transfer function to a single nth order differential equation is equally straightforward. ω in rads or s-1 as an output can be approximately described by a first-order differential equation.
Therefore the transfer function for the angular velocity is Ωs V ss 30 s2 62s300. Consider a generic first order transfer function given by. 81 In the Laplace domain the transfer function is given by ωs Ps. To find the transfer function first write an equation for Xs and Ys and then take the inverse Laplace Transform. PD Control of Second Order System Process and controller transfer functions Ps b s2 a1s a2 Cs kp kds Closed loop transfer function from reference to output Gyrs PC 1 PC bkds kp s2 a1 bkds a2 bkp Closed loop system of second order controller has two parameters. The parameter has the dimension of V a k-1 s-2. This model is linear as long as ft is not a function of x thus it can be transformed into a transfer function This type of transfer function is known as a first order lag with a steady state gain of 10.

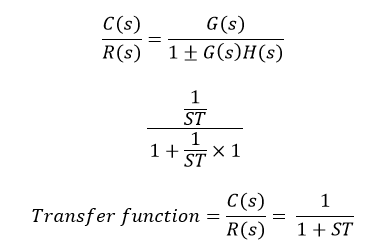


















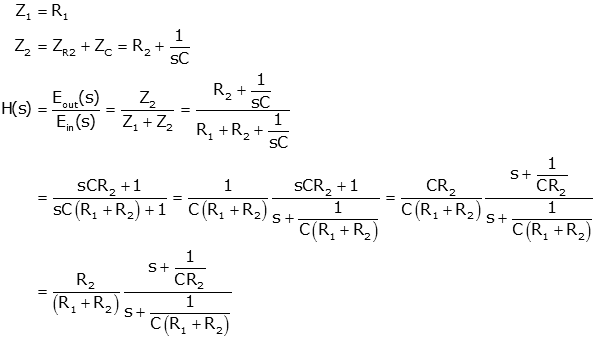







Post a Comment for "First Order System Transfer Function"